Tan2x Formula

An essential trigonometric function is tan2x. The Tan2x formula, which is a frequently utilized double angle trigonometric formula, can be represented using many trigonometric functions, including tan x, cos x, and sin x. Since we already know that tan x is the ratio of the sine to the cosine function, another way to define the tan2x identity is as the ratio of sin to cos.

The tan2x and tan^2x formula, its proof, and its expression in terms of several trigonometric functions are covered in this article. Along with the idea of tan square x, we will also examine the graph of tan2x and its period and solve instances to have a better understanding.

What is Tan2x in Trigonometry?

Trigonometric functions like tan2x have a formula that can be utilized to solve a variety of trigonometric problems. Tan2x is a crucial trigonometric formula for double angles, or angles that have been doubled. It can also be stated as a ratio of sin2x to cos2x, or in terms of tan x. We can write tan2x as the reciprocal of cot 2x, or tan2x = 1/cot2x, as the reciprocal of tan x is cot x. Let’s look at the tan2x equation:

Tan2x Formula

The tan2x formula has two possible expressions. It can be stated solely in terms of the tangent function or as a sine and cosine function combination. The following is the formula for tan2x identity:

• tan2x = 2tan x / (1−tan²x)
• tan2x = sin 2x/cos 2x

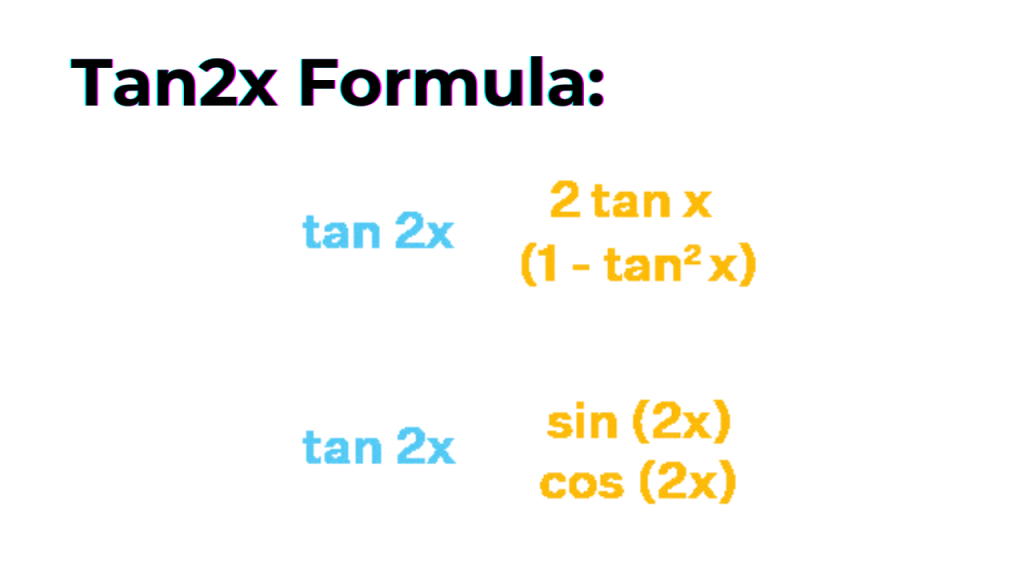
Tan2x Formula Proof

There are two ways to obtain the Tan2x formula. To obtain the tan2x identity, we shall first apply the angle addition formula for the tangent function. Keep in mind that the double angle 2x can be expressed as 2x = x + x. The formula for tan2x will be demonstrated using the trigonometric formula below:

                               tan (a + b) = (tan a + tan b)/(1 – tan a tan b)

We have

tan2x = tan (x + x)

= (tan x + tan x)/(1 – tan x tan x)

= 2 tan x/(1 – tan²x)

As a result, we have used the tangent function’s angle sum formula to obtain the tan2x formula.

Tan2x Identity Proof Using Sin and Cos

We shall now express tan as a ratio of sin and cos in order to obtain the tan2x formula. The following trigonometric formulas will be applied:

• tan x = sin x/ cos x
• sin 2x = 2 sin x cos x
• cos 2x = cos²x – sin²x

Using the above formulas, we have

tan2x = sin 2x/cos 2x

= 2 sin x cos x/(cos²x – sin²x)

Divide the numerator and denominator of 2 sin x cos x/(1 – 2 sin²x) by cos²x

tan2x = [2 sin x cos x/cos²x]/[(cos²x – sin²x)/cos²x]

= (2 sin x/cos x)/(1 – sin²x/cos²x)

= 2 tan x/(1 – tan²x)

As a result, by expressing it as a ratio of sin 2x and cos 2x, we have derived the tan2x formula.

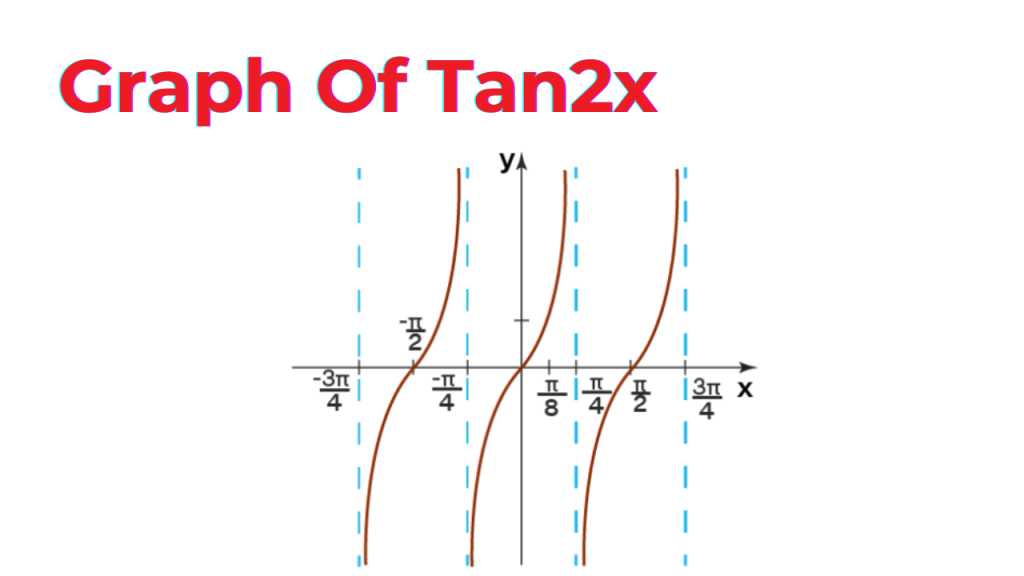
Tan2x Graph

Tan x and tan2x’s graphs resemble each other. We are aware that π is the period of tan x. Given that π/|b| provides the period of tan bx, π/2 represents the period of tan 2x. As we can see from the graph, which is provided below, the value of tan2x repeats every π/2 radians. Furthermore, as tanx is always equal to zero when x is an integral multiple of π, tan2x is also always equal to zero when 2x = nπ, where n is an integer. This suggests that the x-intercepts of the graph below are located at x = nπ/2.

Tan^2x (Tan Square x)

The square of the trigonometric function tanx is tan^2x. The trigonometric identities and formulas that comprise tan^2x can be utilized to obtain the tan square x formulas. Since we already know that tan x can be written as the product of sin and cos, we can also write tan^2x as the product of sin squared x and cos squared x. We may simplify trigonometric formulas and solve intricate integration and differentiation problems using the tan^2x formula. We will determine and go over the tan square x formula in the following part.

Tan^2x Formula

We now have a trigonometric identity that suggests tan^2x = sec^2x – 1, since 1 + tan^2x = sec^2x. Since the sine and cosine functions may be used to describe tan x, we can also write tans square x as the ratio of sin square x and cos square x, leading to the formula tan^2x = sin^2x / cos^2x. Additionally, since we know that tan x is cot x’s reciprocal, we may write tan^2x = 1/cot^2x. As a result, the tan^2x formula list is:

• tan^2x = sec^2x – 1 ⇒ tan²x = sec²x – 1
• tan^2x = sin^2x / cos^2x ⇒ tan²x = sin²x/cos²x
• tan^2x = 1/cot^2x ⇒ tan²x = 1/cot²x

Tan2x in Terms of Cos

The tan2x formula can be obtained in terms of cos. The trigonometric formulas shown below will be used to translate tan2x into terms of cos x.

• tan x = sin x/ cos x
• sin 2x = 2 sin x cos x
• cos 2x = 2 cos²x – 1
• sin x = √(1 – cos²x)

Using the above formulas, we have

tan2x = sin 2x/ cos 2x

= 2 sin x cos x/(2 cos²x – 1)

= [2 √(1 – cos²x) cos x/(2 cos²x – 1)]

Similarly, we can write tan2x in terms of sin using the trigonometric identities.

tan2x = [2 sin x/(1 – 2 sin²x)]√(1 – sin²x)

Important Notes on Tan 2x Formula

• tan2x = 2tan x / (1 − tan²x)
• tan2x = sin 2x/cos 2x
• The derivative of tan2x is 2 sec²(2x)
• The integral of tan2x is (-1/2) ln |cos 2x| + C or (1/2) ln |sec 2x| + C.

Tan2x Examples

 

1. Example 1: Determine the value of tan2x if tan x = 4/3.

   Solution: We know that tan2x = 2tan x / (1 − tan²x). If tan x = 4/3, we have tan²x = 16/9.

   tan2x = 2tan x / (1 − tan²x)

   = 2(4/3)/(1 – 16/9)

   = (8/3)/(-7/9)

   = -24/7

   Answer: tan2x = -24/7

    

2. Example 2: Find the value of tan2x if sin x = 12/13 and cos x = 5/13

   Solution: We know that tan2x = sin 2x/ cos 2x

   = 2 sin x cos x /(cos²x – sin²x)

   = [2 × (12/13) × (5/13)] / [(25/169) – (144/169)]

   = (120/169) / (-119/169)

   = -120/119

   Answer: tan2x = -120/119

3. Example 3: Evaluate the derivative and integral of tan2x.

   Solution: We know that the derivative of trigonometric function tan x is given by sec²x. The derivative of tan2x can be calculated using different methods such as the chain rule and quotient rule. Let us determine the derivative of tan2x using the chain rule.

   d(tan2x)/dx = d(tan 2x)/d(2x) × d(2x)/dx

   = sec²2x × 2

   = 2 sec²(2x)

   Now, we will determine the integral of tan2x. We know that the integral of tan x is -ln |cos x| + C or ln |sec x| + C. Using the formulas of integration, the integral of tan2x is given by,

   ∫ tan2x = (-1/2) ln |cos 2x| + C

   = (1/2) ln |sec 2x| + C

   Answer: Hence the derivative of tan2x is 2 sec²(2x) and the integral of tan2x is given by (-1/2) ln |cos 2x| + C or (1/2) ln |sec 2x| + C.

FAQs on Tan2x Formula

What is Tan2x in Trigonometry?

The Tan2x formula, which is a frequently utilized double angle trigonometric formula, can be represented using many trigonometric functions, including tan x, cos x, and sin x. Tan2x is generally calculated as follows: tan2x = 2tan x / (1 − tan2x).

What is Tan2x Formula?